中国地质大学(武汉)华人策略研究论坛
“科研成果快报”
1. 标题
· Discovering frequent movement paths from taxi trajectory data using spatially embedded networks and association rules
· 基于空间图和关联规则的出租车轨迹数据频繁移动路径挖掘
2. 成果信息
· Wenhao Yu*. Discovering frequent movement paths from taxi trajectory data using spatially embedded networks and association rules. IEEE Transactions on Intelligent Transportation Systems, 2019, 20 (3), 855-866.
3. 成果团队成员
· 禹文豪,博士,中国地质大学(武汉)华人策略研究论坛,副教授,主要从事地图综合、空间数据挖掘和智慧城市应用等研究。(联系邮箱:ywh_whu@126.com;个人网站:http://grzy.cug.edu.cn/yuwenhao/zh_CN/index.htm)
4. 成果介绍
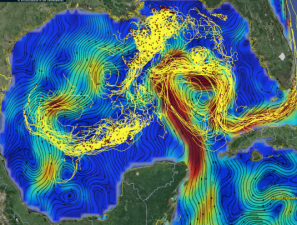
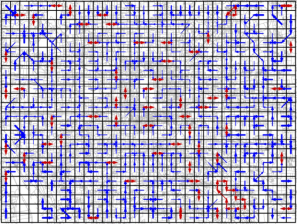
环流是海洋科学的基础问题,其直接影响海洋能量和物质的交换,无论是从全球尺度分析大洋环流对海洋生态系统的影响,还是从局域尺度探讨海洋温度的时空变化,都离不开对环流路径的识别;相比较环流对海洋系统的作用,交通流在城市空间中同样起到能量输送和空间交互的作用(图1)。受以上问题的启发,本文提出一种空间图和关联规则支持下的城市空间“环流”探测方法。
环流是针对固定路径的频繁交互模式,因此,该方法首先规则剖分目标空间,以此获得所有路径的节点或位置;然后通过加载出租车轨迹数据,构建城市空间的交通流图结构,其弧段代表区域(cell)与区域(cell)间的交通联系(图2)。一组连续的、权重值高的弧段集合组成一个潜在的交通“环流”,本文通过采用标签传播聚类方法可识别固定时间段的“环流”路径(图3)。交通流具有高度的动态性,为发现跨越不同时段的频繁“环流”路径,本文进一步引入关联规则挖掘技术,即定义空间图的每条弧段为一个项(item),各个时刻存在的每条路径为一个事务(Transaction),以此由Apriori算法发现跨越各个时段的频繁路径模式。借鉴海洋环流对物理海洋的应用研究,本文获得结果也可作用于城市系统的分析研究,如日常出行轨迹等。
(a) (b)
图 1. 海洋环流与交通频繁路径比较。(Blue lines indicate the type of ‘path’ with different origin and destination, and red lines indicate the type of ‘cycle’ with the same origin and destination.)
(a) (b)
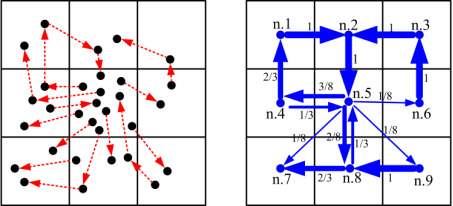
Fig. 2. Example of the modeling of travel flows: (a) raw taxi trajectory data, (b) spatially embedded flow network with edge weight (arrows’ thickness) equal to corresponding probabilities of movement between sub-regions.
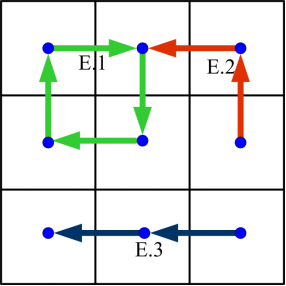
Fig. 3. Identifying the movement paths in the spatially embedded network as presented in Fig. 2, by using Algorithm 1. E.1 (green lines), E.2 (red lines) and E.3 (black lines) are the movement paths obtained from the trajectory data.

Fig. 4. Frequent movement paths during the whole time period with cell size 1 km × 1 km, time interval 1 hour, and support threshold 0.0008.